Met de Euler-Poincaréformule en de Euleroperatoren hebben we in principe de belangrijkste hulpmiddelen geformuleerd om veelvlakken te beschrijven. Voordat diverse beschrijvingen uit de vaklitteratuur tegen het licht worden gehouden, zullen we eerst een paar vingeroefeningen met de Euleroperatoren doen. Dit puur om de formules een beetje in de vingers te krijgen, het Fingerspitzgefühl te ontwikkelen.
Een tetraëder (regelmatig viervlak) bestaat uit –inderdaad- vier vlakken, zes ribben en vier hoekpunten:
(1)

Uit het niets ontstaat (→A) een (massieve) tetraëder (1) -bijvoorbeeld- als volgt:
(2) Msfv: s=1
[grondvlak plus tophoek, inclusief de schil]
(3) 3*Mev: v=4
[met drie keer de operatie Mev wordt het grondvlak omlijnd, inclusief aanbrenging van de driehoekspunten]
(4) 3*Mfe: e=6, f=4, l=4
[hiermee zijn de opstaande vlakken en ribben aangebracht]
N.B. Voor (2) tot en met (4) geldt dat na de dubbele punt “:” telkens aantallen welke corresponderen met waardes uit regel 2 van (1) staan vermeld. Dus bijvoorbeeld “Msfv: s=1″ betekent dat er één shell is, welke in regel 2 van (1) de waarde “-2” heeft.
Om aantallen van waardes te onderscheiden zijn de symbolen voor aantallen cursief weergegeven, terwijl de waardes regulier gedrukt zijn. Bijvoorbeeld: l=4 impliceert de waarde l=-4.
Na (2) is de schil aangebracht, na (3) zijn alle vier hoekpunten aangebracht en na (4) zijn alle ribben en vlakken aangebracht.
Met de juiste Killoperaties kan het viervlak weer geheel worden gedemonteerd, dus terug naar af: A →. Dat wil zeggen:
(5) 3*Kfe
(6) 3*Kev: e=0
(7) Ksfv: s=0, f=0, l=0
Vanuit het massieve viervlak (1) maken we een massieve kubus (8 hoekpunten, 12 ribben en 6 vlakken):
(8) 
Regel 4 uit (8) geeft de verschillen in waardes aan tussen een massieve kubus en en massieve tetraëder. Dus de verschillen tussen de waardes uit regel 3 en de waardes uit regel 2.
De volgende Euleroperatoren zijn toegepast:
(9) 4*Mev: v=8
[de acht hoekpunten van de kubus zijn aangebracht]
(10) 2*Mfe: f=6, l=6, e=12
[de zes vlakken en de twaalf ribben van de kubus zijn aangebracht]
N.B. Voor (9) en (10) geldt dat na de dubbele punt “:” de aantallen die corresponderen met waardes uit regel 3 van (8) staan vermeld als deze anders zijn dan die uit regel 2. Dus die van de shell (s) en de gaps (g) worden niet vermeld, want blijkens regel 4 zijn die niet veranderd.
Hiermee is een kubus vanuit een tetraëder door middel van Euleroperaties tot stand gekomen: tetraëder →kubus
Het is niet moeilijk de weg terug, kubus →tetraëder, uit te voeren met behulp van de juiste Killoperatoren.
De kubus uit (8) is massief, we maken deze nu hol:
(11)

We zien dat alle waarden verdubbeld worden (van acht naar zestien hoekpunten, etc.). Met name komt er ook een schil om de holte erbij.
De volgende operaties zijn in het spel:
(12) Msfv: s=2
(13) 7*Mev: v=16
(14) 5*Mfe: f=12, l=12, e=24
(15)
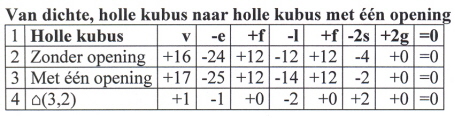
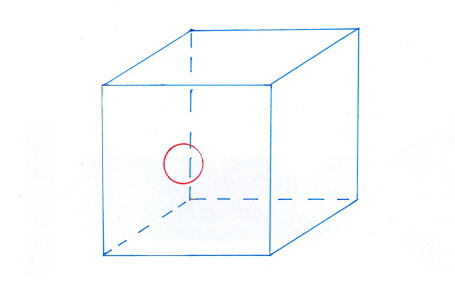 De opening is een ‘rondje’ dat bestaat uit één hoekpunt en één ribbe; zowel aan de ‘binnenkant’ als aan de ‘buitenkant’ van de wand van de holle kubus is er een lus of loop (l) om de opening heen. De opening heeft dus twee lussen. De opening bestaat evenwel uit slechts één ribbe (e) en één hoekpunt (v).
De opening is een ‘rondje’ dat bestaat uit één hoekpunt en één ribbe; zowel aan de ‘binnenkant’ als aan de ‘buitenkant’ van de wand van de holle kubus is er een lus of loop (l) om de opening heen. De opening heeft dus twee lussen. De opening bestaat evenwel uit slechts één ribbe (e) en één hoekpunt (v).
In de tekening is in het rondje van de opening geen hoekpunt getekend. In een latere post meer hierover.
De opening maakt dat de ‘binnenruimte’ van de kubus deel uit gaat maken van de ‘buitenwereld’ en daarin als het ware oplost: het aantal schillen gaat daarmee terug van twee naar één.
De operatoren, tengevolge waarvan de holle kubus zonder opening er één wordt met een opening:
(16) Mfe
(17) 2*Mev
[De opening is omlijnd door één ribbe (e) en één hoekpunt (v)]
(18) Ksfv: s=1, v=17
(19) 2*KeMl: e=25, l=14
(20)

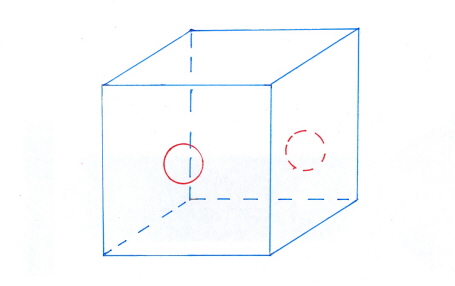
Een gat impliceert twee openingen. De volgende operatoren bewerkstelligen de overgang van (15) naar (20):
(21) Msg: g=1
(22) Mfe
(23) 2*Mev
(24) Ksfv: v=18
(25) 2*KeMl: e=26, l=16
Tot dusverre hebben we langs gebaande wegen de theorie gevolgd, inclusief een paar vingeroefeningen. In de volgende post wordt een nieuw inzicht gepresenteerd. Overigens blijven we daarmee wel, zal worden vastgesteld, binnen de grenzen van de Euler-Poincaréformule, zelfs binnen binnen de grenzen van de Eulerformule.
Lees meer


