De twee voorafgaande posts, Lasnaadconstructie en Laspuntconstructie betroffen (al dan niet vermeende) uitzonderingen op de formule van Euler, welke door Hessel in 1832 zijn beschreven. Eerder nog in 1810 heeft Louis Poinsot twee uitzonderingen beschreven. Later duiken die twee uitzonderingen weer op in een boek van Schläfli. Wij knopen daarop aan.
In deze post worden zaken opnieuw uit de doeken gedaan die al eerder behandeld zijn. Zoals de formule van Euler en de formule van Euler-Poincaré. Enerzijds komt het doordat dit verhaal (wat u nu leest) al eens door mij is opgeschreven voordat ik wist dat deze weblog ooit zou verschijnen. Anderzijds heb ik dat zo gelaten omdat het verhaal zo beter is te volgen.
Op de webpagin’s van Wolfram met betrekking tot de Kleine Stervormige Dodecaëder en de Grote Dodecaëder wordt er op gewezen dat Schläfli de desbetreffende dodecaëder niet erkent als een regelmatig driedimensionaal lichaam.
Ik citeer:
Schläfli (1901, p. 134) did not recognize the small stellated dodecahedron [c.q. the great dodecahedron] as a regular solid because it violates the polyhedral formula, instead satisfying
N0 – N1 + N2 = 12 – 30 + 12 = -6
where N0 is the number of vertices, N1 the number of edges, and N2 the number of faces (Coxeter 1973, p. 172).
De “polyhedral formula” is de formule van Euler (gepubliceerd in 1752), welke ook wel wordt genoteerd als:
(1) V – E + F = 2
(V is het aantal vertices, E is het aantal edges en F is het aantal faces van een veelvlak).
De formule van Euler heeft in principe betrekking op lichamen zonder gaten. Later heeft Lhuilier in 1865 de formule uitgebreid voor de gevallen dat er gaten in het spel zijn:
(2) V – E + F = 2 – 2g
G betreft het aantal gaps.
Weer later heeft Poincaré (gepubliceerd in 1895) een formule gegeven waarin ook rekening wordt gehouden met holtes binnen een lichaam. Een holte is een ruimte, omsloten door vlakken: een afgesloten binnenruimte.
Deze formule beschrijven we in de volgende paragraaf.
Opgemerkt kan worden dat dodecaëders (Grote, Kleine Stervormige of de platonische) doorgaans geen gaten bevatten.
Wel zij vastgesteld dat zowel de Kleine Stervormige (KSD) als de Grote Dodecaëder (GD) tengevolge van doorsnijdingen van de vlakken holtes bevatten.
Hieruit volgt:
In de volgende paragraaf formuleren we de formule van Euler-Poincaré (deze is de door Poincaré uitgebreide formule van Euler).
De formule van Euler-Poincaré
Op een webpagina van het MIT wordt de formule van Euler-Poincaré beschreven en met voorbeelden toegelicht.
De formule luidt als volgt:
(3) V – E + F – (L-F) – 2(S – G) = 0
Een aantal symbolen kwamen we al eerder tegen:
V = aantal hoekpunten, E = aantal ribben, F = aantal vlakken en G = aantal gaten. In onze beschouwing gaan we uit van G = 0.
Nieuw zijn de symbolen L en S.
L staat voor aantal loops (lussen). Met elk vlak correspondeert altijd één outer loop. Als een vlak ontbreekt of onderbroken wordt dan correspondeert daarmee een inner loop. L is dan groter dan F. Op de pagina van het MIT worden voorbeelden van inner loops gegeven. Wij gaan hier niet op in, voor ons zijn deze niet van belang: dat wil zeggen voor de dodecaëders zoals hier behandeld geldt L=F.
S staat voor aantal shells. Een compact lichaam heeft altijd één schil; S=1. Een doos heeft twee schillen: S=2. De buitenkant van de doos heeft namelijk één schil, de holle binnenkant impliceert nog één schil. Dus buiten- plus binnenkant zijn twee schillen.
Een eenvoudige toepassing van de formule van Euler-Poincaré betreft een compacte kubus:
(4) v=8, e=12, f=6, l=6, g=0:
v-e+f-(l-f)-2(s-g)=8-12+6-(6-6)-2(1-0)=0
Is een kubus niet compact, maar hol:
(5)
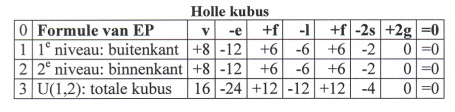
Aan de keerzijde van elk vlak van het eerste niveau is er een vlak van het tweede niveau.
Een analoog voorbeeld is dat van een regelmatig twaalfvlak met holle binnenkant:
(6)
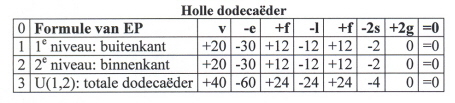
In de volgende paragraaf passen we formule van Euler-Poincaré toe op de Kleine Stervormige Dodecaëder.
De Kleine Stervormige Dodecaëder
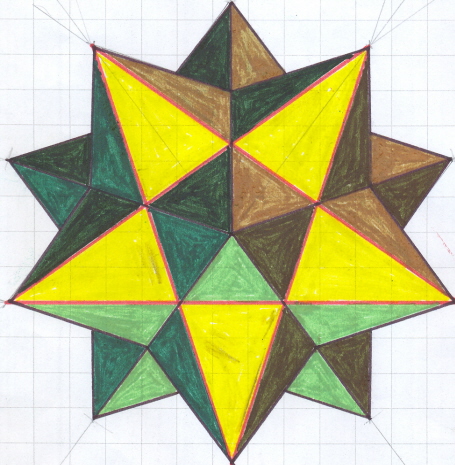
Afbeelding (7):
de Kleine Stervormige Dodecaëder
Ontleend aan oorpronkelijk ontwerp en concept van Tom Ruen; SVG-creatie Júlio Reis
Figuur (7) zullen we in eerste instantie beschrijven à la Schläfli:
(8)

Alles wat van dezelfde kleur is, representeert één van de twaalf vlakken die elkaar doorsnijden. Dus de driehoekige vlakken die door opdeling tengevolge van de doorsnijdingen van twaalf vijfvijfhoekige vlakken er zijn worden om zo te zeggen niet in rekening gebracht. Zo ook worden de ribben en hoekpunten die deel uitmaken van de driehoeken niet meegeteld. Alleen de ribben en hoekpunten die deel uitmaken van de twaalf vijfhoeken worden geteld. Vandaar tabel (8).
Als we de figuur beschrijven in termen van de formule van Euler-Poincaré, dat wil zeggen we houden rekening met holtes tengevolge van de vlakken die elkaar doorsnijden, dan komen we tot het volgende.
De Kleine Stervormige Dodecaëder omvat drie niveaus. Te weten:
Aan de buitenkant toont de KSD zich als een geheel van twaalf aaneengeschakelde vijfkantige torenspitsen, die congruent zijn. In het midden van afbeelding (7) zien we zo’n vijfkantige torenspits.
Zou elke torenspits vervangen worden door een vlak dan toonde de “getransformeerde” KSD zich aan de buitenkant als een regelmatige twaalfvlak, een platonische dodecaëder. Dat wil zeggen twintig hoekpunten, dertig ribben en twaalf vlakken. (a)
Evenwel in de KSD is elk van de zojuist genoemde twaalf vlakken in werkelijkheid een torenspits, bestaande uit vijf opstaande vlakken, vijf opstaande ribben en één hoekpunt, de spits. Dus dragen de twaalf torenspitsen tesamen bij: twaalf hoekpunten, zestig ribben en zestig vlakken. (b)
(a) + (b): v – e + f = (20+12) – (30+60) + (0+60).
De buitenkant heeft per definitie één schil: s=1, dus -2s=-2
Elk zo’n binnenkant is een piramide met een vijfhoekig grondvlak. Dus per binnenpiramide: zes hoekpunten, tien ribben en zes vlakken. Er zijn twaalf van zulke piramiden. Dus in totaal: v – e + f = 72 – 120 + 72.
Er zijn twaalf holle piramides, dus: s=12, -2s=-24.
Aan de keerzijde van elk grondvlak van een piramide uit het tweede niveau is een zijvlak van één binnendodecaëder (een regelmatige twaalfvlak in het binnenste van de KSD). Dus voor het derde niveau geldt:
v – e + f -2s = 20 – 30 + 12 – 2.
Samengevat in (9):
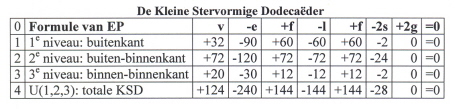
In totaal zijn er veertien schillen, waarvan dertien een holte betreffen.
Besluit
1) Zou de beschrijving zoals in tabel (9) zicht beperken tot het eerste niveau dan was de figuur beschreven als een compact ding; dat zo beschreven ook in overeenstemming is met de formule van Euler.
2) Zou het derde niveau compact (en de piramides van het tweede niveau hol) zijn dan waren er geen veertien, maar dertien schillen.
3) De beschrijving à la Schläfli is een interpretatie van de formule van Euler. De formule van Euler is, hoe deze ook wordt geïnterpreteerd, niet geschikt om een figuur met holtes te beschrijven. En zoals we in de eerste slotopmerking schreven: als de figuur wordt opgevat als een compact ding dan kan ze wel degelijk in termen van Euler worden beschreven. Wordt het opgevat als een hol ding dan kan het alleen adequaat worden beschreven in termen van Euler-Poincaré.
